Factorization is the easiest thing. It is really easy to mess up but it is also easy to do when you know all the rules and how to apply them (see what I did there).
The Number 1 Rule of Factorization (Common Factors)
The first thing we do when we factorize is look for common factors.
$$7x^2 - 3x$$
So to factorize this we just look for a common factor (x in this case) and we cannot go any further
$$x(7x-3)$$
Difference of 2 Squares
$$x^2 - y^2 = (x-y)(x+y)$$
So we take the square root of each square and +, - but why is that? Is it just a magical formula I must learn? Of course not.
$$(x-y)(x+y) = x^2 + xy - xy - y^2$$
See if we expand this then we always + and - the same middle term so it disappears and this is where the concept of the difference of two squares comes from.
E.g.
$$100x^3y - xa^2y$$
You might look at this and be confused but remember what the number 1 rule is?
$$=xy(100x^2 - a^2)$$
Ah we can take out a common factor of xy.
Now:
$$=xy((10x)^2-(a)^2) = xy(10x-a)(10x+a)$$
Quadratic Expressions
If there are only 2 terms for example then look at the first example I gave at the top of this post.
For things that look like this:
$$x^2+6x+5$$
So we look at the last sign. It's positive. Oh so if we have two brackets (_+_)(_+_) or (_-_)(_-_) then these are the only two that will make a positive number for that 5.
$$x^2+6x+5$$
Now look at the first sign. It's also positive. The terms that we add are either both positive or both negative so in this case we will choose both to be positive since there is a +6
$$=(x+5)(x+1)$$
Note that the last two numbers have to make the 5 at the end when multiplied together
$$x^2- 6x +5$$
Oh so in this case we say
$$=(x-1)(x-5)$$
$$2x^2-25x-13$$
The negative here means that we have - and +.
The 2 has to go with one of the x's
$$(2x +1 )(x -13)$$
The more you practice this the better you will get but you need to think about where to put things and you can multiply out at the end to see if your answer is right.
For this one above we have a negative first sign so we know that the larger number needs to be the - one and since we are looking for negative 25 it makes sense that -2(13)+1 = -25.
Four Terms?
$$-x^2 - 2x - x -2$$
Try to factorize two terms and see if we can take out a common factor.
$$-x(x+2) -1(x+2)$$
$$=(x+2)(-x-1)$$
$$-(x+2)(x+1)$$
See how I took (x+2) out.
These are the basics of factorization. There are some more advanced forms of factorization but you need these as a foundation.
Do You Even Math?
I explain mathematical concepts in the simplest ways possible. The goal is to help you gain a deeper understanding of the subject so that you can apply yourself to any problem.
Sunday, September 20, 2015
Monday, September 7, 2015
Straight Line Graphs (y=mx+c)
This post will serve as an introduction to straight line (linear) graphs and the Cartesian Plane. I will explain what the Cartesian Plane is and show you how to plot straight lines using the equation of a straight line as well as how to find the equation of a straight line by just looking at the graph.
What is a straight line?
This seems like a silly question but in Mathematics, there are some misconceptions about what I straight line really is. A Straight Line is any line that connects two points together but it is important to note any restrictions on the length of the line because it can either have a finite length (specific length) or it can extend infinitely and never end.
The Equation of a Straight Line
$$y=mx+c$$
This is the standard equation of a straight line where:
$$\text{m = the gradient / slope of the line}$$
$$\text{c = the y-intercept of the line} $$
$$\text{y = the y-coordinate of a specific}$$
$$\text{point on the graph}$$
$$\text{x = the corresponding x-coordinate}$$
$$\text{at the point on the graph}$$
The Cartesian Plane
This is a sketch of the Cartesian Plane in 2-dimensions. We can also sketch it in 3-dimensions or more but we will just focus on 2-dimensions for this post. The vertical axis is called the x-axis and the horizontal axis is called the y-axis. I have put little lines to represent intervals. You should label them with values that change proportionately.
I will give you two examples to show what I mean:
This is a Cartesian Plane where with intervals of 1. You can see where the negatives are on the sketch above.
This is a Cartesian Plane with intervals of 5.
Plotting points on the Cartesian Plane
If you are plotting a point on the Cartesian Plane, you would write the point as follows:
$$(x,y)$$
where we replace x with the x-coordinate of the point and y with the y-coordinate of the point.
Example: Lets plot the points $$ A(0,0), B(3,6), C(5,-2), D(-3,4),$$ $$E(-2,-3) $$ You would sketch the Cartesian Plane and the points would be plotted as follows:
Quadrants
There are 4 quadrants in the 2-dimensional Cartesian Plane. They are as follows:
What is a straight line?
This seems like a silly question but in Mathematics, there are some misconceptions about what I straight line really is. A Straight Line is any line that connects two points together but it is important to note any restrictions on the length of the line because it can either have a finite length (specific length) or it can extend infinitely and never end.
The Equation of a Straight Line
$$y=mx+c$$
This is the standard equation of a straight line where:
$$\text{m = the gradient / slope of the line}$$
$$\text{c = the y-intercept of the line} $$
$$\text{y = the y-coordinate of a specific}$$
$$\text{point on the graph}$$
$$\text{x = the corresponding x-coordinate}$$
$$\text{at the point on the graph}$$
The Cartesian Plane
I will give you two examples to show what I mean:
Plotting points on the Cartesian Plane
If you are plotting a point on the Cartesian Plane, you would write the point as follows:
$$(x,y)$$
where we replace x with the x-coordinate of the point and y with the y-coordinate of the point.
Example: Lets plot the points $$ A(0,0), B(3,6), C(5,-2), D(-3,4),$$ $$E(-2,-3) $$ You would sketch the Cartesian Plane and the points would be plotted as follows:
There are 4 quadrants in the 2-dimensional Cartesian Plane. They are as follows:
If you look at the points from the example above:
\( A(0,0) \) is in between all the quadrants so we generally just work with it as if it is in Quadrant 1 (it does not matter).
\( B(3,6) \) is in Quadrant 1.
\( C(5,-2) \) is in Quadrant 4.
\( D(-3,4) \) in in Quadrant 2.
\( E(-2,-3) \) is in Quadrant 3.
Plotting a Straight Line on the Cartesian Plane
In order to plot a straight line on the Cartesian Plane we need to plot at least 2 points and then draw a straight line through these points.
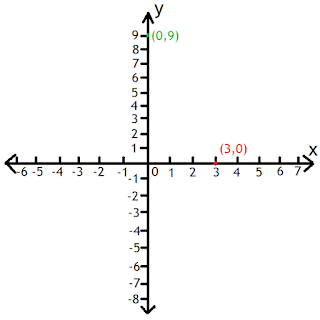
By convention, we try and find the x-intercept (where the graph cuts the x-axis, \( y=0 \) ) and y-intercept (where the graph cuts the y-axis, \( x=0\) ) as these points.
Example: Find the equation of the line \( y = -3x + 9 \)
y-intercept (x=0)
$$y = -3(0) + 9$$
$$y=9$$
$$(0,9)$$
x-intercept (y=0)
$$0 = -3x+9$$
$$3x = 9$$
$$\frac{3x}{3} = \frac{9}{3}$$
$$x=3$$
$$(3,0)$$
So when we plot these points we get:
Now we draw a straight line through these 2 points and label it \( y = -3x + 9 \):
Note that if they give you only 1 point and either m or c then you can substitute the point and solve the equation to get m or c and then you will have the equation of the line and you can draw the graph the same way as above.
Example: \( E(3,4) \) is a point on the line \( y = -x + c \). Find c and then sketch the graph.
Substitute the point E(3,4) into the equation
$$4 = -(3) + c$$
$$4 = -3 + c$$
$$4+3 = c$$
$$c=7$$
\( y = -x + 7 \) is the equation of the graph
y-intercept (x=0)
$$y= -(0) + 7$$
$$y=7$$
$$(0,7)$$
x-intercept (y=0)
$$0= -x + 7$$
$$x=7$$
$$(7,0)$$
So the graph looks like:
Finding the Equation of a Straight Line by using the Graph
You need to have 2 points (or be able to see exactly where they are and could be intercepts but do not need to be) so that we can calculate the gradient. You may be able to see the y-intercept but we can also find it by substitution.
Example: You are given 2 points \( E(-1, -\frac{9}{7}) \) and \(F(2, \frac{33}{7}) \). Find the equation of the straight line that goes through these 2 points.
Plot the points and draw a line through them
Calculate the gradient / slope
The Gradient (m) of a straight line is the slope characterized by the change in y-coordinates over the change in x-coordinates. It is always constant (the same) when dealing with a straight line!
$$m = \frac{\Delta y}{\Delta x}$$
where \( \Delta \) means change.
$$m = \frac{y_2 - y_1}{x_2 - x_1}$$
In this Example, we need to choose which point is the 1st and which is the 2nd (It doesn't matter). Say E is the 1st and F is the 2nd. We write:
$$m_{EF} = \frac{y_F - y_E}{x_F-x_E}$$
if you say \( m_{FE} = \frac{y_E - y_F}{x_E - x_F} \) you will get the same answer. Try it!
$$m_{EF} = \frac{\frac{33}{7} - (- \frac{9}{7})}{2 - (-1)}$$
$$= \frac{(\frac{42}{7})}{3}$$
$$\frac{6}{3} = 2$$
$$y = 2x + c$$
Substitute in a point (any). Say \( E(-1, -\frac{9}{7}) \)
$$-\frac{9}{7} = 2(-1) + c$$
$$-\frac{9}{7} = -2 + c$$
$$-\frac{9}{7} + 2 = c$$
$$c = -\frac{9}{7} + \frac{14}{7}$$
$$c = \frac{5}{7}$$
$$y = 2x + \frac{5}{7}$$
which is the equation of the straight line so we are finished.
Restrictions on the Domain
The way we have been drawing these straight lines uses an assumption that \( x \in \mathbb R \) (i.e. x is any element of the real number system).
Lets use a simple example of \( y = x + 1 \)
Note that x can be any real number and it extends to numbers you cannot see on the graph by showing with arrows that the graph continues.
Restrictions on x
Lets say for example:
a) x = {-1, 0 , 1} then the graph would look like:
In this case. These 3 points make up the entire graph with a restricted domain.
b) \( x \in [-1,1] \) or \( -1 \leq x \leq 1 \). The graph would look like:
where the graph does not continue.
Note that similar restrictions are possible on the y-values but when we restrict the y-values, we say we are restricting the range instead of domain.
Friday, September 4, 2015
Fractions
Many people struggle with fractions. It is important to know all the rules and how to apply them because the reason people struggle with this section is that they do not know these rules.
I have used numbers when explaining these rules for the first time. Please note that all of these rules still apply when using algebraic expressions such as x and y.
I have used numbers when explaining these rules for the first time. Please note that all of these rules still apply when using algebraic expressions such as x and y.
What is a fraction?
$$2 \div 3 = \frac{2}{3}$$
Writing '2 divided by 3' is the same thing as writing '2 over 3' in the form of a fraction.
$$\frac{\text{Numerator}}{\text{Denominator}}$$
The Numerator is the expression at the top of a fraction.
The Denominator is the expression at the bottom of a fraction.
Types of Fractions
A Proper Fraction is a fraction where the Numerator is smaller than the Denominator. It is called proper because it represents a fraction of a whole.
$$\frac{1}{2}$$
This represents 50% or 0.5 which makes 'proper' sense in terms of it being a 'fraction'. Therefore it is called a Proper Fraction.
An Improper Fraction is a fraction where the Numerator is greater than the Denominator. It is called improper because it represents more than just a fraction of a whole.
$$\frac{2}{1}$$
This represents 200% or 2 which does not make 'proper' sense in terms of this being a 'fraction' but it does make mathematical sense where we just have more than one whole. Therefore it is referred to as an Improper Fraction
A Mixed Fraction is an improper fraction written in a different way. We take the number of whole numbers separately and just show the remainder as a proper fraction.
$$\frac{5}{2} = \frac{4}{2} + \frac{1}{2} = 2 \frac{1}{2}$$
Please note that \( 2 \frac{1}{2} \not = 2 \times \frac{1}{2} \) although many people think it is because of the way that it is written!
Simplifying Fractions
The best way to simplify fractions (without a calculator) is to divide both the numerator and denominator (fraction must remain unchanged) by the biggest number that you can think of that will go into both the numerator and denominator without any remainder. If you are not in simplest form then you can divide by another number until you are.
$$\frac{27}{36} = \frac{27 \div 3}{36 \div 3} = \frac{9}{12}$$
$$= \frac{9 \div 3}{12 \div 3} = \frac{3}{4}$$
Now the fraction is in its simplest form.
Adding & Subtracting Fractions
When Adding Fractions, we need to find the LCD (Lowest Common Denominator) which is a denominator that can be common for all of the fractions we are adding together. You can the simply add all the numerators over this common denominator.
$$\frac{1}{2} + \frac{3}{8} = \frac{1 \times 4}{2 \times 4} + \frac{3}{8}$$
$$= \frac{4}{8} + \frac{3}{8} = \frac{4+3}{8} = \frac{7}{8}$$
Did you see how we multiplied the top and bottom of the fraction by 4 to get the denominator to be 8 without changing the fraction (since we multiply and divide by the same number).
When Subtracting Fractions, the approach is the same but replace the + signs with - signs.
$$\frac{1}{2} - \frac{3}{8} = \frac{1 \times 4}{2 \times 4} - \frac{3}{8}$$
$$= \frac{4}{8} - \frac{3}{8} = \frac{4-3}{8} = \frac{1}{8}$$
Multiplying Fractions
When Multiplying Fractions, we multiply the Numerators of the fractions and the Denominators of the fractions together.
$$\frac{2}{5} \times \frac{3}{2} = \frac{2 \times 3}{5 \times 2} = \frac{6}{10} = \frac{3}{5}$$
Note that we can also cancel / simplify numerators with denominators of other fractions when fractions are multiplied together.
$$\frac{\not 2}{5} \times \frac{3}{\not 2} = \frac{3}{5}$$
Dividing Fractions
When Dividing Fractions, it is always best to use the Tip and Times Rule (you swap the numerator and denominator of the second fraction around and change the sign from \( \div \) to \( \times \) ).
$$\frac{3}{2} \div \frac{5}{2} = \frac{3}{2} \times \frac{2}{5}$$
$$= \frac{3}{ \not 2} \times \frac{\not 2}{5} = \frac{3}{5}$$
Exponents / Roots
An Exponent / Root that is applied to an entire fraction can be applied to both the numerator and denominator separately.
$$\sqrt{\frac{4}{100}} = \frac{\sqrt{4}}{\sqrt{100}} = \frac{2}{10} = \frac{1}{5}$$
\( \sqrt{\frac{4}{100}} \) means 'square root of 4 over 100'. This can be extended to cube roots, 5th roots, 12th roots, etc.
Note that \( (10)^2 = 10 \times 10 = 100 \) so \( \sqrt{100} = \sqrt{10 \times 10} = 10 \)
\( 10^2 \) means 'ten squared'. This can be extended to to cubed, to the power of 4, to the power of 5, to the power of a billion, etc.
$$(\frac{3}{10})^3 = \frac{3^3}{10^3} = \frac{3 \times 3 \times 3}{10 \times 10 \times 10}$$
$$= \frac{27}{1000}$$
An Improper Fraction is a fraction where the Numerator is greater than the Denominator. It is called improper because it represents more than just a fraction of a whole.
$$\frac{2}{1}$$
This represents 200% or 2 which does not make 'proper' sense in terms of this being a 'fraction' but it does make mathematical sense where we just have more than one whole. Therefore it is referred to as an Improper Fraction
A Mixed Fraction is an improper fraction written in a different way. We take the number of whole numbers separately and just show the remainder as a proper fraction.
$$\frac{5}{2} = \frac{4}{2} + \frac{1}{2} = 2 \frac{1}{2}$$
Please note that \( 2 \frac{1}{2} \not = 2 \times \frac{1}{2} \) although many people think it is because of the way that it is written!
Simplifying Fractions
The best way to simplify fractions (without a calculator) is to divide both the numerator and denominator (fraction must remain unchanged) by the biggest number that you can think of that will go into both the numerator and denominator without any remainder. If you are not in simplest form then you can divide by another number until you are.
$$\frac{27}{36} = \frac{27 \div 3}{36 \div 3} = \frac{9}{12}$$
$$= \frac{9 \div 3}{12 \div 3} = \frac{3}{4}$$
Now the fraction is in its simplest form.
Adding & Subtracting Fractions
When Adding Fractions, we need to find the LCD (Lowest Common Denominator) which is a denominator that can be common for all of the fractions we are adding together. You can the simply add all the numerators over this common denominator.
$$\frac{1}{2} + \frac{3}{8} = \frac{1 \times 4}{2 \times 4} + \frac{3}{8}$$
$$= \frac{4}{8} + \frac{3}{8} = \frac{4+3}{8} = \frac{7}{8}$$
Did you see how we multiplied the top and bottom of the fraction by 4 to get the denominator to be 8 without changing the fraction (since we multiply and divide by the same number).
When Subtracting Fractions, the approach is the same but replace the + signs with - signs.
$$\frac{1}{2} - \frac{3}{8} = \frac{1 \times 4}{2 \times 4} - \frac{3}{8}$$
$$= \frac{4}{8} - \frac{3}{8} = \frac{4-3}{8} = \frac{1}{8}$$
Multiplying Fractions
When Multiplying Fractions, we multiply the Numerators of the fractions and the Denominators of the fractions together.
$$\frac{2}{5} \times \frac{3}{2} = \frac{2 \times 3}{5 \times 2} = \frac{6}{10} = \frac{3}{5}$$
Note that we can also cancel / simplify numerators with denominators of other fractions when fractions are multiplied together.
$$\frac{\not 2}{5} \times \frac{3}{\not 2} = \frac{3}{5}$$
Dividing Fractions
When Dividing Fractions, it is always best to use the Tip and Times Rule (you swap the numerator and denominator of the second fraction around and change the sign from \( \div \) to \( \times \) ).
$$\frac{3}{2} \div \frac{5}{2} = \frac{3}{2} \times \frac{2}{5}$$
$$= \frac{3}{ \not 2} \times \frac{\not 2}{5} = \frac{3}{5}$$
Exponents / Roots
An Exponent / Root that is applied to an entire fraction can be applied to both the numerator and denominator separately.
$$\sqrt{\frac{4}{100}} = \frac{\sqrt{4}}{\sqrt{100}} = \frac{2}{10} = \frac{1}{5}$$
\( \sqrt{\frac{4}{100}} \) means 'square root of 4 over 100'. This can be extended to cube roots, 5th roots, 12th roots, etc.
Note that \( (10)^2 = 10 \times 10 = 100 \) so \( \sqrt{100} = \sqrt{10 \times 10} = 10 \)
\( 10^2 \) means 'ten squared'. This can be extended to to cubed, to the power of 4, to the power of 5, to the power of a billion, etc.
$$(\frac{3}{10})^3 = \frac{3^3}{10^3} = \frac{3 \times 3 \times 3}{10 \times 10 \times 10}$$
$$= \frac{27}{1000}$$
Subscribe to:
Posts (Atom)